![\includegraphics[height=2in]{pie}](img3.png)
|
Hal R. Varian1
University of California, Berkeley
August 1999 (revised: August 29, 2000)
The INDEX Project is an experiment designed to estimate how much people are willing to pay for various kinds of Internet Quality of Service (QoS). The INDEX designers architected the system to provide different QoS's on demand and to record the usage of each different QoS by each user. Users can change their requested QoS instantaneously and are billed monthly for their usage. From April 1998 to December 1999 we provided approximately 70 users at UC Berkeley with residential ISDN service through the INDEX Project.
Edell and Variaya (1999) provides an overview of the project. Current information and other reports can be found on the INDEX project Web page.
In this paper I examine one set of INDEX experiments designed to measure the willingness to pay for bandwidth. In these experiments users were offered the choice of 6 different bandwidths, ranging from 8 Kbs to 128 Kbs. Users could choose 8 Kbs service for free at any time. Each Sunday a new set of prices were chosen for the other bandwidths, ranging from .1 cents to 12 cents per minute of use. The INDEX system measured how much bandwidth subjects consumed at each different price, allowing experimenters to estimate demand for different bandwidths as a function of the price vector.
Figure 1 depicts a pie chart of total usage. About 3/4 of the usage was 8 Kbs service. Since 8 Kbs was free, users tended to keep it on all the time. Usage was roughly equally divided among the other 5 bandwidths with positive prices.
Table 1 depicts the output of regressing the log of total minutes used on the log of the 5 different prices. Observations with zero usage were omitted. The coefficients in these log-log regressions can be interpreted as price elasticities of demand. Coefficients printed in bold are statistically significant at the 95% level.
|
Note that the diagonal terms (the own-price effects) are all negative and statistically significant. The subdiagonal terms are the cross-price effects for lower bandwidths. The positive numbers indicate that one-step lower bandwidths are substitutes for the chosen bandwidth.
This sign pattern is quite plausible. It is also worth noting that the implied elasticities are rather large. The regression for 96 Kbs service implies that a 1% increase in the price of 96 Kbs leads to a 3.1% drop in demand, and a 1% increase in 128 Kbs service leads to a 1.7% increase in the demand for 96 Kbs service.
We ran these regressions with and without dummy variables for the
individual users, with little change in the estimated coefficients.
Table 2 depicts the ![]() s for these regressions.
s for these regressions.
|
Roughly speaking about 20 percent of the variance in demand is explained by price variation, about 75 percent of the variance in demand is explained by individual specific effects, and about 5 percent is unexplained. These fits are remarkably good, giving us some confidence that the subjects are behaving in accord with the traditional economic model of consumer behavior.
The reduced form estimates given above suggest that the users are behaving in an economically sensible way. Hence it makes sense to try to model their choice behavior in more detail so we can extrapolate to other environments.
W adopt a very simple behavioral model, and assume that users get
utility from the bits transferred (![]() ) and the time (
) and the time (![]() ) it takes
to transfer them. The cost of transfer time has two components: the
subjective cost of time (
) it takes
to transfer them. The cost of transfer time has two components: the
subjective cost of time (![]() ), which varies according to users and
circumstances, and the dollar cost, which depends on the chosen
bandwidth (
), which varies according to users and
circumstances, and the dollar cost, which depends on the chosen
bandwidth (![]() ). If
). If ![]() is the chosen bandwidth, optimization
implies that
is the chosen bandwidth, optimization
implies that
Since bandwidth is by definition bits per unit time, we have ![]() .
Making this substitution and canceling the
.
Making this substitution and canceling the ![]() s, we have
s, we have
It follows from simple algebra that
Figure 2 depicts these bounds graphically. Define the
``total cost of time'' by
![\includegraphics[height=2in]{time}](img19.png)
|
We assume that the user's time cost is a random parameter, drawn from
a distribution ![]() . Sometimes the user is in a hurry, which means
he or she has a high cost of time. Sometimes they are patient, which
means the user has a low cost of time. This distribution of time cost
is summarized by the probability distribution
. Sometimes the user is in a hurry, which means
he or she has a high cost of time. Sometimes they are patient, which
means the user has a low cost of time. This distribution of time cost
is summarized by the probability distribution ![]() and our objective
is to estimate this distribution.
and our objective
is to estimate this distribution.
Each weekly menu of prices and bandwidths gives us a set of upper and
lower bounds. Since we observe the frequency with which the user
chooses bandwidth ![]() during a week, we can construct a histogram for
each user for each week illustrating the implied time costs. An
example for a particular user in a particular week is given in Figure
3
during a week, we can construct a histogram for
each user for each week illustrating the implied time costs. An
example for a particular user in a particular week is given in Figure
3
![\includegraphics[height=2in]{histo}](img21.png)
|
Table 3 shows the frequency with which the upper and lower bounds fall in a give range. For example, 39 of the users, or about 60%, have an average upper bound on the time cost of less than 1 cent a minute, 8 of the users, or about 12%, have an average upper bound greater than 1 cent a minute, but less than 2 cents a minute and so on. The last line in this table is the distribution of simple average of the upper and lower bounds which is a rough-and-ready, nonparametric estimate of the distribution of time cost across the population.
|
The remarkable thing about Table 3 is the low values that users place on their time. Most of the users have a time cost of less than 1 cent a minute. However there are a few users with systematically higher time costs.
The obvious question is whether we can predict which users have higher
time value. Relevant variables available are occupation type, income, and
whether the employer or the user pays for the service. We found that
occupational dummies do a pretty good job of explaining the time costs
using the following regression:
This suggests that the time value is relatively predictable using available demographic data. For those who prefer graphs, Figure 4 shows the distribution of time values by occupational classification, which tells almost the same story as the regression. However, it must be cautioned that University of California employees may not be representative of the population as a whole, although they may be representative of early adopters of new technology.
In an earlier section, we showed how to derive observed bounds on the
cost of time. If we observe ![]() choices, we can construct a data set
choices, we can construct a data set
![]() for
for ![]() . If
. If ![]() is the true
distribution from which the data have been drawn the probability of
observing
is the true
distribution from which the data have been drawn the probability of
observing ![]() in the region
in the region
![]() is given by
is given by
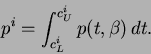
We can estimate the parameter ![]() that makes the probability,
that makes the probability,
![]() , close to the observed frequency,
, close to the observed frequency, ![]() . Various measures of
closeness could be used, but a convenient one this context is the
Kullbec-Leibler entropy measure:
. Various measures of
closeness could be used, but a convenient one this context is the
Kullbec-Leibler entropy measure:
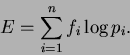
We choose a truncated Normal distribution for the parametric form of
th distribution ![]() . Figure 5 illustrates the
fitted distribution and the five corresponding histograms. Figure
6A is a bit less messy; it depicts the empirical CDF
constructed using the upper bounds, along with the theoretical CDF
implied by the estimated parameters.
. Figure 5 illustrates the
fitted distribution and the five corresponding histograms. Figure
6A is a bit less messy; it depicts the empirical CDF
constructed using the upper bounds, along with the theoretical CDF
implied by the estimated parameters.
![\includegraphics[height=2in]{fit2}](img37.png)
|
We could also fit the CDF directly. Figure 6B shows the theoretical CDF that minimizes the sum of squared residuals between it and the corresponding frequencies, along with the estimated parameters. Note that they are not very different from the entropy-maximizing estimates.
We applied this technique to estimate the implied parameter values for all 70 or so subjects. For about 7 subjects, the fits exhibited numerical instability. In about half of these cases, the instability was due to the fact that the user always chose the highest speed. The estimates of time value for the other cases tended to be quite low, consistent with the nonparametric results. We do not report these results since they tell essentially the same story as the nonparametric results.
Encouraged by the results described in the previous section, we estimated the CDF that minimizes the sum of squared residuals over the entire data set. The results are depicted in Figure 7. Note that the average cost of time (over the population) is very low, as would be expected from the previous results.
These results raise the immediate question as to why the time costs are so low. A time cost of 1 cent a minute is only 60 cents an hour. Lots of student jobs at Berkeley are available for $10-$12 an hour, so this number is far below prevailing wage rates, even for students.
Several hypotheses suggest themselves.
The INDEX experiment is the first experiment to systematically estimate the demand for Internet bandwidth. Our estimates indicate very low willingness-to-pay for bandwidth, and very low values for time. We offer some reasons why these values may make sense, but our ultimate conclusion is that our sample of users was not willing to pay very much for bandwidth, at least given today's set of applications.