Offprint of: M.K. Buckland (1972). Are Obsolescence and Scattering related? Journal of Documentation, 28(3), pp. 242-246.

L’obsolescence et la diffusion sont-elles liées?, French translation by Pinar Cytheree, July 2108.
Се освесенство и разбирање поврзани?, Macedonian translation by Katerina Nestiv, May 2019.
*New* Czy obsolescencja i rozproszenie są powiązane ze sobą?, Polish translation completed by Jodi Williams, TheWordPoint, May 2023.
A obsolescência e a disposição relacionadas?, Portuguese translation by Artur Weber and Adelina Domingos, Nov 2017.
Sunt uzura morală şi împrăştierea legate?, Romanian translation by eWorldSports, March 2019.
Связаны ли устаревание и рассеяние?, Russian translation by Angelina Baeva, Feb 2019.
*New* ¿Están relacionadas la obsolescencia y la dispersión?, Spanish translation by Chema Bescos, Agencia de traducción Ibidem Group, Feb 2023.
Це застарівання і розсіювання пов'язано?, Ukrainian translation by A2Goos team

ARE OBSOLESCENCE AND SCATTERING RELATED?

Considerable attention has been paid, in this journal and elsewhere, to each of two aspects of the use of literature. One of these is the relative decrease in use of material as it ages ('obsolescence') which has been discussed by Brookes [1] and many others [2]. The other aspect is the extent to which the use of material tends to be concentrated in a few titles ('Bradford's Law of scattering') , which has been treated by Bradford [3], Leimkuhler [4], Brookes [5], and Fairthorne [6].

Cole [7] perceived that these two 'laws', especially when examined in conjunction, had significant implications for deciding how large library collections should be. This area has been analysed in more depth by Buckland and Woodburn [8] and by Brookes [9]. In brief, these analyses give some insight into the economics of library stock policies with respect to the number of journal titles held and the length of time they are retained. They are also relevant to the management of indexing and abstracting services in that they indicate the loss of coverage which could be expected to resulti from the exclusion of older and more marginal literature. In each case it is assumed that there is an ascertainable pattern of obsolescence which is known to vary from subject to subject. It is also assumed that the scattering effect can be estimated and that this will also vary from one subject to another.

The possibility that there might be some relationship between these two variations appears to have been neglected. Are they related? It would be of considerable theoretical interest if a relationship could be established and much data collection could be avoided if one could be deduced from the other. At the University of Lancaster Library Research Unit, when the implications of scattering and obsolescence policies with respect to the number of journal titles held and the length of time they are retained. They are also relevant to the management of indexing and abstracting services in that they indicate the loss of coverage which could be expected to resulti from the exclusion of older and more marginal literature. In each case it is assumed that there is an ascertainable pattern of obsolescence which is known to vary from subject to subject. It is also assumed that the scattering effect can be estimated and that this will also vary from one subject to another.

The possibility that there might be some relationship between these two variations appears to have been neglected. Are they related? It would be of considerable theoretical interest if a relationship could be established and much data collection could be avoided if one could be deduced from the other. At the University of Lancaster Library Research Unit, when the implications of scattering and obsolescence appears to have been neglected. Are they related? It would be of considerable theoretical interest if a relationship could be established and much data collection could be avoided if one could be deduced from the other. At the University of Lancaster Library Research Unit, when the implications of scattering and obsolescence theoretical interest if a relationship could be established and much data collection could be avoided if one could be deduced from the other. At the University of Lancaster Library Research Unit, when the implications of scattering and obsolescence theoretical interest if a relationship could be established and much data collection could be avoided if one could be deduced from the other. At the University of Lancaster Library Research Unit, when the implications of scattering and obsolescence were being explored during 1967 and 1968, an attempt was made to see if there was any evidence of a relationship. The results were indicative but not conclusive. Other research interests have taken priority and the purpose of this note is to describe what was done in the hope that researchers engaged in bibliometric analysis may be able to pursue this topic further.

It is convenient to discuss scattering and obsolescence in terms of the compactness of literatures. A highly obsolescent literature such as physics is more compact with respect to time than the literature of geology. Similarly, some literatures are more compact with respect to scattering than others. The initial hypothesis had been that scattering and obsolescence tend to vary inversely. For example, some literatures might tend to be wide and short (widely scattered over a broad front of journals, but obsolescent in a short time) whereas others might be narrow and long (narrowly concentrated in a few journals but long-lived, i.e. obsolescing only slowly). This is represented graphically in Fig. 1a.

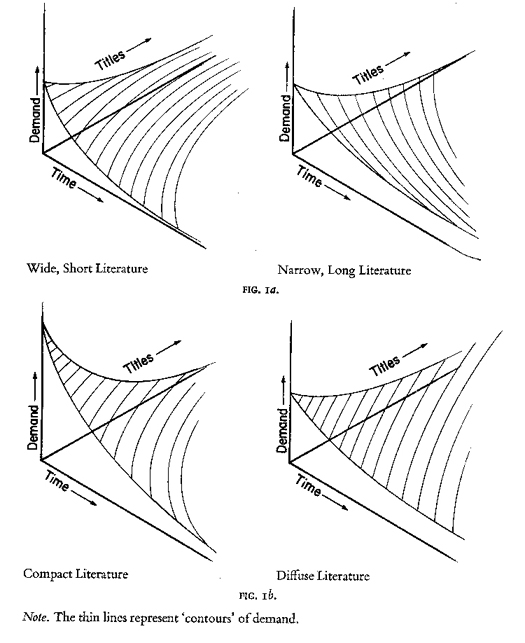
An alternative hypothesis was that scattering and obsolescence tend to vary directly. For example, some literatures tend to be compact (narrowly concentrated in a few journals and obsolescent in a short time) whereas others are diffuse (widely scattered over a broad front of journals and long-lived, i.e. obsolescing only slowly). This is depicted in Fig. 1b. In order to get comparable data for different subjects, reference was made to Brown's Scientific serials [10]. This contains analyses of itations at the ends of articles published during a period of about eighteen months in each of eight scientific subjects: Mathematics, Physics, Chemistry, Geology, Physiology, Botany, Zoology, and Entomology. The citations from journals in each subject were sorted by journal to give scatter and by age to give obsolescence. The data is presented raw and no attempt was made to fit curves to the results. In fact, Brown's commentary mixes absolute measures and proportions. For example, his Table 16 gives the proportion of each sample covered by the most productive 100 journals, even though the sample sizes vary enormously. It would have been more appropriate to have examined the proportion of each sample covered by a given proportion of the journals.

Brown's data were analysed and obsolescence was plotted against scattering for each of the eight subjects. The results, which are presented in Fig. 2, are clearly at variance with the original hypothesis that scattering and obsolescence vary inversely. Instead they show a tendency for them to vary directly. The data clearly imply that compactness with respect to time is associated with concentration with respect to scattering.

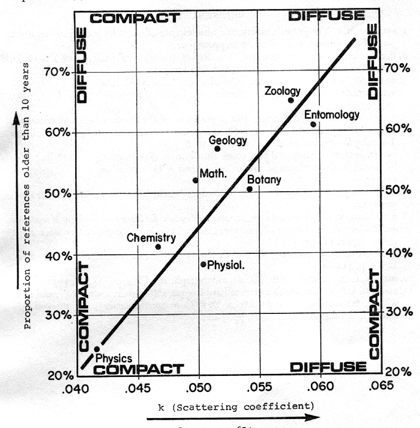
Fig. 2. Compactness of Literatures

The scattering coefficient k is taken from Cole's formulation of Bradford's law of scattering [7]
R_n=R_N(1 + k log n/_N)
where R_n is the number of references in the most productive n journals in a literature wherein N journals contribute R_N references. The values of k which are given are based in each case on the value of R_n which constitutes 90% of R_N. Data from Brown.[10]

A note of caution should be made concerning this finding. In some subjects the source journals chosen contributed more citations than in others. For example the leading chemistry journals contributed 10,052 citations whereas the leading zoology journals contributed 1,819. There is, in fact, a correlation between the sample size and the two kinds of compactness. The 'compact' subjects are those with the larger number of citations in their samples. The implications of this are not clear. Scattering and obsolescence patterns would appear to be 'non-dimensional', in the sense that one would expect a random sample from either distribution to form a distribution of the same shape. Nevertheless, Professor E. T. O'Neill has suggested* that there may be an element of dimensionality in that small sample sizes lead to the computation of scattering coefficients which over-estimate the true amount of scattering. Such a bias could explain, at least partially, the correlation between sample size and literary compactness with respect to scattering. An alternative explanation of the correlation with sample size is that a highly concentrated literature needs to have relatively bulky journals in the nuclear zone and that this bulk determines the size of samples picked by Brown's method.

Assuming that some literatures are more compact than others, one wonders why this should be. Dr A. Hindle has suggested that the compactness of literatures might be related to a subject's 'hardness' or 'softness'; that is to say, the extent to which the terminology and hypotheses are clearly definable and the problems are highly structured. In this respect physics is generally regarded as more 'hard' than biology. The rankings of the subjects with respect to compactness in Fig. 2 do seem to agree roughly with subjective impressions of the relative hardness and softness of the subjects concerned. Quite independently, Professor de Solla Price has advanced the theory that obsolescence is related to hardness and softness and can be used as a hardness index [11].

REFERENCES

1. BROOKES, B. C. The growth, utility, and obsolescence of scientific periodical literature. Journal of Documentation, vol. 26, 1970, pp. 283-94.

2. For a convenient review see : JAIN, A. K Report on a statistical study of book use, Ph.D. thesis. Purdue University, Lafayette, Ind. (PB 176 525).

3. BRADFORD, S. C. Documentation. London, Crosley Lockwood. 1948.

4. LEIMKUHLER, F. F. The Bradford distribution. Journal of Docurnentation, vol. 23, 1967, pp. 197-207.

5. BROOKES, B. C. The derivation and application of the Bradford-Zipf